Regularization.
Regularization is a regression technique that prevents or regulates the estimated coefficient from shrinking to zero. In other words, one does not encourage the formulation of more complex or flexible models to reduce the risk of overfitting.
Another way into it is being through regularization, which allows us to throw away less important features so that the model can perform better with unseen inputs.
So, it is about reducing the cost for validation loss in addition to improving correctness in the model.
It introduces a penalty on the model with large variance; thus, reducing the beta coefficients towards zero makes it prevent overfitting.
There are two types of regularization in Machine Learning
LASSO regularization
Regression)-What is Lasso Regularization (L1)?
It stands for Least Absolute Shrinkage and Selection Operators
It adds L1 the penalty
L1 is the sum of the absolutes value of the beta coefficient
SSE + λ∑|βi|
λ = penalty
βi = slope of the curve
The goal here is as follows: If λ = 0, we get the same coefficients as linear regression. If λ is big, all coefficients are driven towards zero.
Regression-What is Ridge Regularization (L2) It adds L2 as the penalty
L2 is the sum of the squared magnitude of the beta coefficients.
SSE + λ∑(βi)^2
λ = penalty
βi = slope of the curve
As the value of λ (lambda) increases, the regression line becomes more horizontal and the coefficient value approaches zero.
Comparative Study of Ridge and Lasso Regression
Regression-What is Ridge Regularization (L2)
It adds L2 as the penalty
L2 is the sum of the squared magnitude of the beta coefficients.
SSE+λ∑(βi)^2
λ = penalty
βi = slope of the curve
As the value of λ (lambda) increases, the regression line becomes more horizontal and the coefficient value approaches zero.
While Lasso may shrink certain coefficients to zero, leading to variable selection, ridge regression will not be able to impose a zero restriction on any coefficient.
Both methods permit the use of correlated predictors, but they treat the problem of multicollinearity differently. Ridge regression treats the two predictors equally, whereas in Lasso regression, some coefficients are assigned larger values than those of the other coefficients.
Lasso is at its most effective in prediction when only a few significant explanatory variables are considered and the rest are close to zero values. Ridge regression essentially works in the opposite direction of lasso. It operates best in high-dimensional data or when having many large and quite similar parameters.
Of course, all the previous two statements are somewhat theoretical aspects because in practice, we do not know the true parameter values. For the relevant model selection with the case in hand, one just needs to run cross-validation. For lasso, ridge, and elastic-net regression, these are regularization techniques widely used in machine learning to prevent overfitting in regression models by adding penalties to model parameters. So, it modifies cost functions, checking the weight estimates of linear regression. Let us define each one of them in detail.
Ridge vs. Lasso Regression
Lasso may set some coefficients to zero, resulting in variable selection, but ridge regression cannot.
Both techniques allow for the use of correlated predictors, but they deal with multicollinearity in different ways:
Ridge regression has identical coefficients for associated predictors, but lasso regression has one bigger coefficient and the rest are practically zeroed.
Lasso performs best when there are a few significant factors and the rest are close to zero.
Ridge performs best when there are numerous large parameters with similar values.
However, in practice, we don’t know the true parameter values, so the previous two points are somewhat theoretical. Just run cross-validation to select the more suited model for a specific case.
Elastic Net
Elastic Net first evolved as a response to criticism of lasso, whose variable selection can be overly dependent on data and thus unstable. The solution is to mix the penalties of ridge regression and lasso to achieve the best of both. Elastic Net seeks to minimize the following loss function:
where α is the mixing parameter between ridge (α = 0) and lasso (α = 1).
Now, there are two parameters to tune: λ and α. The glmnet package can tune λ using cross-validation for a fixed α, but does not support α-tuning, thus we will use caret for this task.
Lasso, Ridge, and Elastic Net regressions are popular regularization techniques in machine learning used to prevent overfitting by adding penalties to the regression models. These techniques work by modifying the cost function used to train the model, constraining the coefficient estimates in linear regression. Let’s explore each of them in detail.
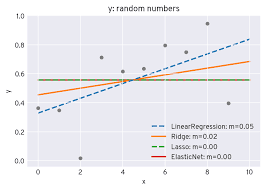
1. Recap on Linear Regression
Linear regression estimates the relationship between a dependent variable (y) and a number of independent variables (X_1, X_2, …, X_n). It attempts to minimize the sum of squares of such errors, that is:
In simple language, this is an error requirement: Objective function (OLS) = min ∑_(i=1)^(n) (y_i-∧y_i)^2. However, simple linear regression may not solve the problem of overfitting with excessive predictor variables, correlated predictors, or those that happen to be significantly high along a single dimension.
However, simple linear regression does not address overfitting, especially in cases with many predictors, correlated variables, or high-dimensional datasets. This is where regularization methods like Ridge, Lasso, and Elastic Net come in.
2. Ridge Regression (L2 Regularization)
Ridge regression addresses overfitting by adding an L2 penalty (the sum of squared coefficients) to the objective function.
Ridge Regression Objective:
[
\text{Objective (Ridge)} = \min \sum_{i=1}^{n} (y_i – \hat{y_i})^2 + \lambda \sum_{j=1}^{p} \beta_j^2
]
Where:
- ( \lambda ): regularization strength (hyperparameter)
- ( \beta_j ): model coefficients
Key Points:
- L2 Regularization penalizes large coefficients by shrinking them toward zero, but never forcing them to zero.
- As ( \lambda ) increases, the model complexity reduces, leading to smaller coefficient values and reduced variance.
- It works well when most predictors are relevant because it retains all variables but shrinks their magnitude.
Advantages:
- Helps in multicollinearity (correlated predictors) by shrinking correlated variables together.
- Useful when there are many small/medium-sized effects.
Disadvantages:
3. Lasso Regression (L1 Regularization)
Lasso regression is adding L1 penalty to the objective function, i.e., sum of the absolute values of coefficients.
Lasso Regression Objective:
[
text{Objective (Lasso)} = \min \sum_{i=1}^{n} (y_i – \hat{y_i})^2 + \lambda \sum_{j=1}^{p} |\beta_j|
]
Where:
• ( lambda ): regularization strength (hyperparameter)
• ( beta_j ): model coefficients
Key Points:
• L1 Regularization forces every coefficient to be equal to zero which acts as a selection of features.
• For big values of ( lambda ), one or the other becomes virtually=- zero; makes Lasso especially useful for sparse models (that is, when only a small subset of predictors is important).
Advantages:
• Automatic feature selections, hence leading to simpler resulting models.
4. Elastic Net Regression (Combination of L1 and L2 Regularization)
Elastic Net regression combines both L1 (Lasso) and L2 (Ridge) penalties to balance the benefits of both techniques.
Elastic Net Objective:
[
\text{Objective (Elastic Net)} = \min \sum_{i=1}^{n} (y_i – \hat{y_i})^2 + \lambda_1 \sum_{j=1}^{p} |\beta_j| + \lambda_2 \sum_{j=1}^{p} \beta_j^2
]
Where:
- ( \lambda_1 ) controls the Lasso penalty (L1 regularization).
- ( \lambda_2 ) controls the Ridge penalty (L2 regularization).
Key Points:
- Elastic Net blends L1 and L2 penalties, making it ideal when dealing with both feature selection and multicollinearity.
- When predictors are highly correlated, Elastic Net can select groups of correlated variables, unlike Lasso, which picks one arbitrarily.
- The model’s performance is sensitive to both penalties, so selecting the right balance between L1 and L2 regularization is crucial.
Advantages:
- Combines the best of Lasso (sparse solutions) and Ridge (grouped selection in multicollinearity cases).
- More flexible than Ridge or Lasso alone, since it can handle a mix of small and large effects.
Disadvantages:
- More complex hyperparameter tuning, as it involves both ( \lambda_1 ) and ( \lambda_2 ).
5. Hyperparameter Tuning in Regularization
Regularization methods involve tuning the regularization strength (( \lambda ) or combination of ( \lambda_1 ) and ( \lambda_2 ) for Elastic Net). Common approaches for tuning include:
- Cross-validation: The data is split into training and validation sets multiple times, and the performance is evaluated to find the best ( \lambda ).
- Grid search: Test a range of values for ( \lambda ) and evaluate the performance.
- Random search: Test random combinations of hyperparameters for efficiency.
6. Practical Use Cases
- Ridge Regression is commonly used when we expect all predictors to have some effect on the target variable and multicollinearity is present.
- Lasso Regression is ideal when you want to perform feature selection and expect many predictors to be irrelevant.
- Elastic Net Regression is a middle-ground approach when you suspect that groups of correlated variables are important, and you need both feature selection and model stability.
7. Mathematical Interpretation of the Penaltie
- Ridge (L2 Penalty): The penalty term constrains the coefficients to be small but typically non-zero. This makes the solution stable when there is multicollinearity.
- Lasso (L1 Penalty): The penalty term results in some coefficients being exactly zero, effectively removing features and making the model sparse.
- Elastic Net (L1 + L2 Penalty): A convex combination of Lasso and Ridge, where the relative importance of the two penalties is controlled by a mixing parameter .
8. Visualizing Regularization Effects
- Ridge (L2):
- Shrinks coefficients uniformly.
- No coefficient becomes zero, but all are smaller.
- Lasso (L1):
- Some coefficients shrink to zero.
- Fewer predictors are retained, leading to feature selection.
- Elastic Net:
- A mix of the effects of Ridge and Lasso.
- Can select correlated features together, unlike Lasso, while still retaining sparsity.
8. Visualizing Regularization Effects
- Ridge (L2):
- Shrinks coefficients uniformly.
- No coefficient becomes zero, but all are smaller.
- Lasso (L1):
- Some coefficients shrink to zero.
- Fewer predictors are retained, leading to feature selection.
- Elastic Net:
- A mix of the effects of Ridge and Lasso.
- Can select correlated features together, unlike Lasso, while still retaining sparsity.
Regularization has a vital role in contemporary data science.
Regularization: Lasso, Ridge, and Elastic Net-R, redefining the regression modeling landscape.
Somewhat intuitively and popularly accepted models suffer from failures in areas when data have high dimensionality and/or are too collinear. This has been a problem more visible where data are complex-here spanning applications from genomics and finance through to marketing and artificial intelligence.
Thus regularization serves to tend to this ailment by penalization on overly complex models. These impound weight limits going into coefficients and thus strike a balance between overfitting and underfitting, leading to good prediction models in previously unseen scenarios. This core principle of balancing complexity with predictive accuracy iscentral to the philosophy of machine learning and underscores the enduring relevance of regularization techniques.
The Lasso Regression: Its Simplicity
By automatic variable selection, Lasso regression is most efficient in the high-dimensional space. Coefficients are shrunk to exactly zero under Lasso, thus greatly simplifying the models; they now become much easier to interpret as well as computationally more efficient. The more simple models usually are more robust and interpretable than their more complex counterparts, thus it is generally held as a parsimony rule.
The Real-Life Benefit of Lasso Regression:
1. Healthcare and Genomics:
E.g., in medical research, it is a common practical example where Lasso regression is used to identify specific genetic markers associated with diseases and reduces data dimension without losing its predictive efficacy.2. Natural Language Processing (NLP):
Since Lasso is utilized in a wide part of text classification tasks, it selects from a thousand possible features those most relevant ones to become part of the model-making efficiency more than 50% to 450%.
But this is not what Lasso has in it. The reason would be the intrinsic feature selection instability it exhibits because it plots the presence of one or multiple features linkages with a highly correlated feature. Practically, this means that Lasso may be termed as a master-selecting algorithm for finding sparse models but missing the interpersonal relationships among predictors.
Ridge Regression: Focusing on Stability
Ridge, on the other hand, includes all predictors into the model without subjecting them to a selection process. Hence, it can be very useful in cases where multicollinearity occurs, as coefficients only get shrunk by proportion. In this way, no one predictor can dominate the model in a very disproportionate manner. Stability is essential in situations where all features have significant importance and cannot be ignored.
Real-time Applications of Ridge Regression:
1. Economic Forecasting:
As predictors, GDP growth, unemployment rates, inflation are always less dependent on each other without including the level of developments made with time; hence they become the initial predictor variables in the economic models. applied to datasets with many irrelevant features, potentially reducing interpretability. For this reason, Ridge is often used in scenarios where interpretability is secondary to predictive accuracy.
An Excellent Combination: Elastic Net Regression
Elastic Net is a kind of hybrid approach which renders Lasso and Ridge regression model together in some ratio to allow space for variable selection but still have stability. Because it uses both L1 (absolute value) and L2 (squared value) penalties, the Elastic Net makes available the flexible handling of complex data sets. Further, it offers a better efficiency over Lasso on correlated features, thus making it famous in real-world applications.
Practical Benefits of Elastic Net: 1. The Equilibrium Between Inclusion/Exclusion and Shrinkage: – Properly addresses arbitrary exclusion by correlated variables avail themselves such that all relevant predictors contribute to the model. 2. Flexibility: – This mixing parameter (α\alphaα) makes it very flexible for fine-tuning the balance between Lasso and Ridge according to the user-specific needs. Practical Applications: 1. Bioinformatics: – Elastic nets are encouraged to assign coordinates with some traits or conditions, as observed across collections of genes in Bioinformatics, where thousands of correlated genes might be present. 2. Marketing Analytics: – Elastic Net could be very useful for customer behavior modeling as much as identifying important predictors in correlated marketing variables to ensure they adhere to stability.
The twin penalties inherent to Elastic Net make it computationally expensive; therefore, careful tuning on hyperparameters (λ\lambdaλ and α\alphaα) is required. Yet, because of its versatility in modeling various datasets, it becomes favorable in the omnipotent bag of many data scientists.
Comparing Lasso, Ridge, and Elastic Net. The major point out of their study is the insight that no one of these techniques is the best for all cases. Lasso, Ridge, and Elastic Net do have their tide according to characteristics that are natural to the specific dataset and the analysis goal.
Criteria Lasso 1:
This comparison draws out the significance of comprehending the strengths as well as weaknesses of each technique which allows practitioners to take decisions according to their actual needs.
Wider Implications and Best Practices
Regularization techniques were no longer mere mathematical tools, but rather a more rounded philosophy of data science. At its heart lies the very importance of balance-simple and complex, accurate and generalizable, selected and retained.
Best Practices for Implementation:
1. Feature Scaling:
Regularization is a function of magnitude only with respect to the coefficients of features. Hence, standardization or normalization of features is necessary for results to be accurate irrespective of what that would mean.
2. Cross-Validation:
The regularization parameter (λ) should be chosen such that it takes into account cross-validation to ensure that the regularized model generalizes well for unseen data.
3. Combination with Other Methods:
This also applies to combining regularization with feature engineering or principal component analysis (PCA) to further improve performance.
4. Interpreting Results:
The overfitting reduced by the regularized models does however require practitioners to do some careful deliberation on the coefficients and what they imply for decisions.
Ethical Considerations:
It is indeed the same with regularization: its use in machine learning raises quite an ethical issue. For instance, under healthcare or criminal justice domains, there may be cases in which Lasso may thereby exclude critical variables, with the end result being discrimination or unjust outcomes. Practitioners have to ensure their models are not only accurately developed but also fair and transparent.
These future forecasting regularized regressions. This is a bit of a butter with releasing encumbering distribution as this machine learning develops along courses time.
There are capabilities of predictive modelling. With the increase of dimensionality and multicollinearity, the types of data such as images, text, genomic sequences and sensor readings have started to demand stronger methods.
Emerging Trends:
1. Combination with Deep Learning
Techniques like L1 and L2 regularization are now very much a part of a neural network to avoid overfitting. Thus, these things will more continue to be relevant.
2. AutoML is becoming an important aspect of almost every framework specific for final goal automation, for model selection, and hyperparameter tuning.
3. XAI
: When the demand for interpretable models increases, sparse representations that Lasso and Elastic Net deliver will play an important role in developing transparent AI.
Final Reflections
Ties the endearing qualities of Lasso, Ridge and Elastic Net into their methods of addressing classic regression problems with a nod to the realities of contemporary data science.
Indeed, these methods are parsimony, stability, and flexibility in an integrative perspective, essential for any professional.
Data scientists interested in analytics do not only build their analytical knowledge horizons through competency in these techniques but also create a larger culture of thoughtful and responsible building of models. At the forefront of these, regularization techniques will continue to be a cornerstone in our efforts to build models that are accurate, interpretable, and impactful.
By the end, real power turns out to be behind Lasso, Ridge.
Actually, Lasso and Elastic Net have proven their strength outside mathematical or theoretical demonstration; they have much more beyond that-they transform the raw data into actionable insight-enabled improvements in lives, discoveries, and the future.
Conclusion
- Ridge Regression is great for preventing overfitting in high-dimensional datasets when all predictors are relevant.
- Lasso Regression shines in scenarios where automatic feature selection is necessary, especially in sparse models.
- Elastic Net provides a balanced approach when you have both correlated predictors and the need for feature selection.
These techniques are highly useful in modern machine learning and offer a way to manage complexity, improve interpretability, and generalize models well to unseen data.

