When is Logistic regression Suitable?
1. If your data is binary
> 0/1, Yes/No, True/False.
2. If you need probabilistic results
3. when you need a linear decision boundary
4. If you need to understand the impact of a feature
Mathematical intuition Must to know for below
1. Logistic Regression Cost function
2. sigmoid function
3. Confusion matrix
4. Precision, Recall & F-score.
Logistic Regression is a supervised machine learning algorithm commonly used for binary classification problems, where the goal is to predict one of two possible outcomes. Despite its name, logistic regression is utilized for classification rather than regression.
Key Concepts of Logistic Regression:
Logistic Regression in Machine Learning: A Comprehensive Guide to Understanding, Applications, and Impact
In the evolving landscape of machine learning, logistic regression continues to be an endpoint technique which balances both ease and utility. In it plays a key role in the solution of classification problems where, even when data of different domains are provided, a decision can be done. At its base this article is shown to be the origin, what the theory of logistic regression is, how it can be applied in practice, and the group of real-world applications of logistic regression. By the end, the readers not only have all the necessary information about logistic regression, but they will also know how influential is has been.
What is Logistic Regression in Machine Learning?
Logistic regression is a supervised learning model whose performance is optimized for binary classification. Compared to the continuous values regularized regression, logistic regression estimates the probability of discrete categories. It is based on the assumption that the association between a dependent variable and one to multiple independent variables can be modelled from a logistic function (i.e., sigmoid function).
Since logistic regression takes as an input the sigmoid function, sigmoid function is the core of logistic regression, and the output of sigmoid function is linear prediction in the probability interval (0~1). This ability makes logistic regression able to score the probability of an event occurring and thus it can be considered as a very powerful tool for classification.
How Logistic Regression Works: A Mathematical Perspective
In practice, the LR is an extension of the linear regression model. It computes weighted sum of input variables, performs weighted sum for which the summation is carried out after the weighted sum of the input variables, performs bias term addition, and then sigmoid, the sum. The mathematical representation is expressed as follows:
σ(z)=11+e−z\sigma(z) = \frac{1}{1 + e^{-z}}σ(z)=1+e−z1
Here, zzz is an affine weighted combination of weights (www) and of input features (xxx).
Z w0 w1x1 w2x2 \dots wnsx nz w0 w1x1 w2x2 \dots wnsx+y.
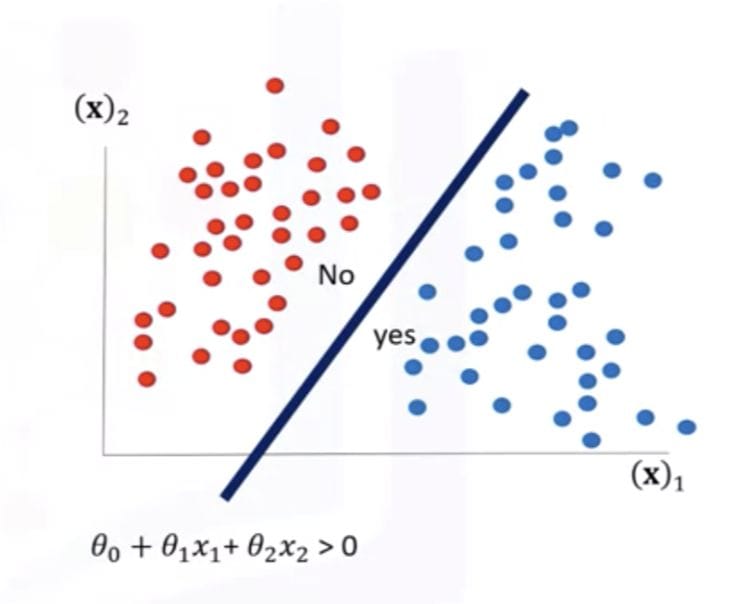
The sigmoid function maps zzz to probability in the range [0, 1], i.e., the desired class probability. The decision threshold (usually 0.5) is used to determine the type predicted. Threshold probabilities belong to the first class if they are above threshold, and to the second class if they are below threshold.
Steps in Logistic Regression:
Key Features and Assumptions of LR
LR assumes a set of conditions for it to be a good tool for classification: .
- Linearity in Log-Odds: LR is a linearly related function between the predictor and the log-odds of the response. This relationship simplifies computation and aids interpretability.
- Independence of Observations: Observed data in the dataset should be mutually independent, therefore estimates of bias will not be shown.
- No Multicollinearity: However, in LR, one also assumes that the independent variables are not highly correlated. Strongly multicollinearity can lead to biased estimates of coefficients of the fitted model and to a poor interpretability of the fitted model.
- Sufficient Sample Size: With a smaller sample size, the parameter estimates are less accurate, meaning both the model is less accurate and the transferability is poor.
It is of great interest to determine the assumptions made by such models in order to construct robust prediction LR models.
Applications of Logistic Regression Across Industries
The flexibility of logistic regression also manifested itself in its wide range of uses across all types of fields. Such utility in addressing classification problems has become extremely important and indispensable for any task, owing to a vast array of applications in healthcare, marketing, etc.
Healthcare and Medicine
Logistic regression is one of those techniques most actively used in healthcare applications, predicting the patients’ outcome, diagnosis, as well as risk prediction. Under the assumption, for instance, that logistic regression models are able to infer the risk that a patient developing the disease will actually develop, the risk of a patient’s developing may be extrapolated to cover information on age at death that is present in death certificates during specific time periods. The current ability in medical practitioners to make informed decisions and to allocate resources in an efficient way comes with the consequence that they now stand to benefit from this predictive power.
Marketing and Customer Segmentation
In customer segmentation and customer development, logistic regression is being employed by marketers.6. According to the purchase data, demographic information and engagement data, the companies can choose and focus on high-value customers and optimize the marketing behaviors respectively. Logistic regression can also be used to predict the risk of customer churn and use this information to help companies implement proactive measures to avoid churn.
Finance and Fraud Detection
Whole for risk model of loan default from the application credit information, the income information and the economic information. Furthermore, models of logistic regression suggest patterns of anomalies in transactions that can be exploited as cues for fraudulent activity.
Social Sciences and Behavioral Research
Researchers in social sciences apply logistic regression to data from surveys to predict human behavior, and to humans or animals to apply the technique. For instance, by means of logistic regression, one can, for example, characterize the effect of variables that influence, e.g., voting, participation in interventions, or a consumption decision.
Advantages of Logistic Regression
One of the advantages of logistic regression is its ease of use and interpretation. It reveals the dependencies among variables, upon which prediction may be done, so that practitioners would be able to understand the source of prediction. In addition, logistic regression is also computationally efficient and not sensitive to overfitting when there is proper scaling of data set.
Another notable advantage is its probabilistic nature. Logistic regression, unlike most other ML algorithms, produces probability, which may be beneficial for tasks dealing with confidence that the decision has to be trustworthy.
Limitations of Logistic Regression and How to Address Them
Interestingly, logistic regression can be used as a powerful tool, however, logistic regression does have its flaws. The bottleneck is the rationale of the linearity assumption. However, if there are nonlinearities between predictors, logistic regression may not be sufficiently flexible to model them accurately. In example, each, a type of feature engineering, or a shift to non-linear search spaces (e.g., decision trees and/or neural networks) are potentially more appropriate.
Logistic regression also needs to be able to take missing data and outliers on board, because these could cause the model to be too optimistic. Data preprocessing methods, including imputation and scaling, are also of equal importance for data quality.
Another limitation is its sensitivity to imbalanced datasets. Logistic regression can use much of the data even when the most frequent class is considerably dominant, by paying a price for the rare vote(s). To solve the problem, there are some ways, such as oversampling minority class, undersampling majority class, or even different performance metrics (for example, F1-score or area under ROC curve).
Logistic Regression vs. Other Machine Learning Algorithms
Logistic regression is frequently compared with more advanced models (decision trees, support vector machines, and neural networks, among others). Although these algorithms may show greater accuracies in certain situation, logistic regression still, as a relatively easy to implement algorithm, a clean algorithm and simple algorithm, is still a very usual algorithm to proceed with.
As compared with black-box models, LR does not just state the feature-relevance order but also provides the feature-relationship between them. Probably most notably, clarity is of a special concern in applications where explainability is considered a critical need, such as health or finance.
Implementing Logistic Regression: A Practical Approach
Logistic regression flowchart various stages, ranging from data preprocessing to model validation. Here’s a typical workflow:
- Data Preprocessing: Clean and preprocess dataset excluding missing data, standardize features, and convert categorical variables to labeled format.
- Model Training: Split the dataset into training and testing sets. Fit logistic regression model using training set and optionally fine tune hyperparameters.
- Evaluation: Compare the model’s performance in the testing set on metrics such as accuracy, precision, recall and the ROC-AUC plot.
- Interpretation: Approximation and inference of the relationships between the features and the target from the model’s parameter coefficients can be realized.
- Optimization: If the model output is not satisfactory, then the feature engineering, regularization or other techniques of the algorithms need to be taken into account.
The Future of Logistic Regression in Machine Learning
Whilst the evolution of sophisticated machine learning algorithms has occurred, logistic regression continues to offer a powerful and interpretable solution for classification work. The capacity to generalize to developments in feature design, data analysis, and computation makes it an issue in modern data science.
Also, logistic regression is a basic algorithm that can help scientists to learn more sophisticated algorithms. Its core principles are woven into a large number of sophisticated methods including deep learning and ensemble learning, which highlight the continued importance of the principles in machine learning.
Deep Dive into Logistic Regression: Advanced Insights and Practical Strategies
No matter how simple in essence, logistic regression, as the basis of machine learning, always brings significant value to the applications it is applied. Because of its statistical weight, mathematical simplicity, and practical relevance, it is the desginated tool of data scientists and machine learning professionals. In this comprehensive search, we will present multifaceted concepts, variants, practical limitations and optimization strategies so as to offer a desirable utilization of logistic regression.
The analysis of the sigmoid function and its application to Logistic Regression.
The sigmoid function is at its core in logistic regression. To each real number there is assigned a value in the interval [0,1] by this mathematical function. The function is expressed as:
σ(z)=11+e−z\sigma(z) = \frac{1}{1 + e^{-z}}σ(z)=1+e−z1
Here, zzz (weighted sum of the input features and their coefficients) bias term. The output is a probability of the item belonging to a do/don’t notion, i.e., (yes/no) class. The differentiability of the sigmoid function is a key property of the sigmoid function and hence gradient-based optimization techniques can be used to train the logistic regression models.
For logistic regression, the decision boundary is defined by applying the sigmoid function. For binary classification, the default threshold is 0.5. However, the threshold can be varied for a particular issue. For example, in the medical diagnostic field, a false negative error rate can cause the threshold to be lowered to optimize the sensitivity).
Multiclass Logistic Regression: Extending Beyond Binary Classification
Although logistic regression is an inherent candidate of the binary classification, it can be generalized to multiclass by the use of one-vs-rest (OvR) and multinomial logistic regression.
• One-vs-Rest (OvR): On this basis, in this framework, for each class a logistic regression model is trained, in which the former is considered positive class and the remaining are negative class. As for class prediction, the class is selected with maximum probability. OverR is simple to use, highly computationally efficient (CC) and potentially uncalibrated for mutually opposite (CCC) probabilities of the considered models.
• Multinomial Logistic Regression: In this technique, the probability of each class is learned jointly by means of the softmax function (i.e., the sigmoid function extended to more than one class). Therefore, MNLR is computationally more expensive, but in general it tends to produce more calibrated probabilities and a unified model for the prediction.
In both strategies, the larger scope of logistic regression is extended to more kinds of problems, ranging from visual recognition to natural language processing.
Regularization in Logistic Regression: Preventing Overfitting
Overfitting is one of the fundamental issues in machine learning, in which a model can fit the training data very closely, yet fit the new data poorly. Logistic regression addresses this by introducing regularization, which is, in a sense, penalizing large coefficients in an attempt to prevent the model from becoming too complex.
• L1 Regularization (Lasso): In this method the modulus of the coefficients are included in the loss function. On the other hand, it also produces sparsity by driving some of the regressor coefficients to 0, and thus it performs the feature selection. In particular, L1 regularization is of great significance in the high-dimensional data set that abounds in irrelevant features.
• L2 Regularization (Ridge): In L2 regularization, sum of the squared coefficients are concatenated to the loss function. It does not artificially force “fringe” large coefficients to zero, but forces them to zero and this in practice yields a more stable model. L2 regularization is successful as long as features are conditionally salient, however contributions are compensated.
• Elastic Net: Elastic Net is a mixture of L1 and L2 regularization, which shares sparsity and robustness of L1 and L2. Above all, since it is employed to high-dimensional data, it is such a fast algorithm for correlated feature set.
One of the advantages of regularization in logistic regression is not only preventing overfitting but also providing the models their interpretability by simplifying the relationships between the predictor variables.
Feature Engineering and Scaling for Logistic Regression
Quality of a good logistic regression model depends heavily on the input variables. Feature engineering and scaling play a key role in the quality of the model and the convergence.
Feature Engineering
Feature engineering refers to the process of creating, transforming or choosing the features in order to realize the best model performance. Common techniques include:
• Interaction Features: Representation of a relation between variables through the learning of the new features as output (or the quotient between the original features).
• Polynomial Features: Adding non-linear transformations of features to capture non-linear relationships.
• Encoding Categorical Variables: Conversion of categorical variables into categorical form, conversion of single-level variables with one-hot encoding, discrete encoding, or target encoding to a categorical format.
Feature Scaling
However, for the logistic regression, there is a large bias in name of the scaling of the input features, also under regularization. Normalizing makes all features equally informative of the model.41. Common scaling techniques include:
• Standardization: Data standardization to mean 0 and standard deviation 1.
• Normalization: Feature scaling to be in the range between 0 and 1 or to be in the range -1 to 1.
Besides speeding up the model convergence, scaling speed also has the effect of stabilizing gradient-based optimization.
Dealing with Imbalanced Data in Logistic Regression
Logistic regression, although it, is one of the most difficult problems in the face of imbalanced datasets, i.e., when one class is orders of magnitude larger than others. In the model, it’s effective for most class, and thus ineffective on minority class. Several strategies address this issue:
• Resampling Techniques: An imbalance data set for each of the two classes by oversampling (i.e., SMOTE) the minority class or the majority class.
• Class Weight Adjustment: Change loss function so that misclassification of minority class will be penalized with a higher penalty.
• Threshold Tuning: Changing decision threshold to enhance sensitivity for minority class.
Evaluation of the performance of a model on imbalanced data set, based on metrics including precision, recall, F1-score, and the area under the precision-recall curve (PR-AUC), gives a good understanding of the trade-off between false positives and false negatives.
Logistic Regression in Real-World Scenarios: Case Studies and Examples
Predicting Customer Churn
Customer retention is one of the main business problems and logistic regression has been widely used for the churn prediction task. Customer behavioral, transactional, and demographic information can be exploited to build logistic regression models that can forecasted customers who are at risk of churn (i.e. They have been used to embedded targeted retention programs that increase efficiency, and improve customers experience.
Credit Scoring in Finance
Creditworthiness is assessed by logistic regressions on banks and financial institutions, respectively. Use of defaults risk estimations for loans, i.e., income, work history, credit coverage, repayment history coverage and so forth, has been taken. Due to the interpretablity of logistic regression, it is a very desired solution in the heavily constrained financial services industry.
Disease Diagnosis in Healthcare
Logistic regression has also been used to develop a disease prediction problem regarding whether a subject’s data suffers from a disease or no disease (i.e., whether a disease condition is present). In other words, the risk of subsequent readmission can be estimated through the patient’s age, cholesterol, blood pressure and more characteristics of each patient, etc. Its utility for risk stratification and treatment decisions in relation to probability estimation has clinical implications beyond the use of risk calculators that assess disease risk.
Interpreting Logistic Regression Models
One of logistic regression’s standout features is its interpretability. Coefficients (www) are log-odds change with one unit change in the feature. Positive coefficient values represent the strength of a feature that increases the probability of positive class, and negative coefficient values represent the strength of a feature that decreases the probability of positive class.
Coefficients can be remapped into odds ratio for ease of interpretation.
OddsRatio=ewOdds Ratio = e^wOddsRatio=ew
Odds ratios offer a more specific quantitative description of the association between an effect and a feature. For instance, an odds ratio value of 2 means that when the feature is increased by 1 unit, the probability of positive class is doubled.
Challenges in Logistic Regression and How to Overcome Them
Multicollinearity
Inversion of independent variables with strong correlation can lead to a biased estimator of the coefficients and therefore to poor interpretabilitie. Multicollinearity is assessed by computing the Variance Inflation Factor (VIF) for each of the variable. In the case where multicollinearity is present, the impact can be overcome by using tools such as principal component analysis (PCA) or feature selection.
Non-Linearity
Besides, based on the idea of the logistic regression, logistic regression also implicitly and tenuous assumption that the interaction expressions of the features are linearly expressed in the log-odds, which may not be valid in reality. Also, the polynomial feature or some type of non-linear transformation allows the finding of complex relationships. However, if not, resampling to alternative non-linear algorithms, e.g., decision trees is also justified.
Outliers
The effect of outcome in logistic regression models may be of interest when regularization is not fixed. Outlier detection and treatment using robust scaling techniques or outlier detection algorithms ensures model robustness.
Optimizing Logistic Regression for Better Performance
Optimization algorithms play an important role for training logistic regression models. The standard paradigm, consisting of an iterative determination of the best value for loss function, gradient descent is modified. Variants (e.g., stochastic gradient descent (SGD), in particular, can be demonstrated to lead to an improvement in both computational efficiency and convergence rate.
Learning rate scheduling is another optimization strategy. Decreasing learning rate that occurs throughout the iterations can accelerate the optimization and avoid the local optimum.
On the other hand, cross-validation does not just hint at a sample generalizability on data that has never seen the data before. When the dataset is partitioned into k folds and then tested on each fold, highly accurate estimates of model performance are achieved and overtraining is prevented.
The Future of Logistic Regression in Machine Learning
Logistic regression continues to be a popular algorithm despite that machine learning era. Due to its applicability to new approaches, such as to feature embeddings or mixed solutions, its utility is guaranteed. In addition, the interpretability of logistic regression is still unmatched in key areas in which interpretability is not waveringly dispensable.
Due to the development of data science, logistic multiple linear regression will be used as an introductory tool for beginners and a sophisticated interpreter for experts. As to the ease of use, flexibility and interpretability, logistic regression is no doubt one of the hits for machine learning practice for the next few decades.
Final Thoughts
Logistic regression, after all, is a realization of the power of simplicity in ML. The use of this with its principle and on its own nature as it views itself is also possible for translation into practice for solution in the wild. In particular, logistic regression offers a basis for which decisions can be made, on the basis of data-driven understanding, for predicting a customer’s behaviour, for diagnosing a disease or for estimation of risk. Its current and future roles underscore its importance in a machine learning toolkit, providing cryptographic safety and practicality.
Conclusion
Logistic regression is a beautiful, yet simple, example of how seemingly simple can be effective in ML. Since it can be used for classification tasks that combine accuracy and interpretability and efficiency, it has become a standard tool for a wide range of applications. For when practitioners reach a point where they are familiar enough with its theoretical framework, and its applicability, and its limitations, they can come to grasp its true value as an entry point into data-driven decision making.
Logistic regression represents the marriage of machine learning, a means, which sustains the future of both success of statistics and possibility of coding. Its external validity points to a crucial requirement for model interpretability, not only for the sake of the model itself, but also to serve as the springboard from which more complex models could be built.

